
RÉSEAU TRIPHASÉ ÉQUILIBRÉ
Un système triphasé est un réseau à trois tensions [courants] sinusoïdales alternatives, de même fréquence, déphasées, les unes par rapport aux autres, d’un angle de 2π/3. 120°
On dit que le système est équilibré si les trois grandeurs sinusoïdales sont de même valeur efficace.
Tension Simple
Tension simple: est la différence de potentiel entre une phase et le neutre. Nous les noterons : v1(t), v2(t) et v3(t)
Les trois tensions simples sont :
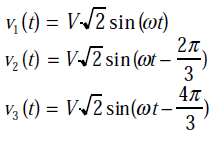
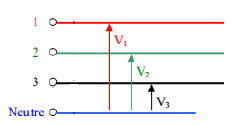
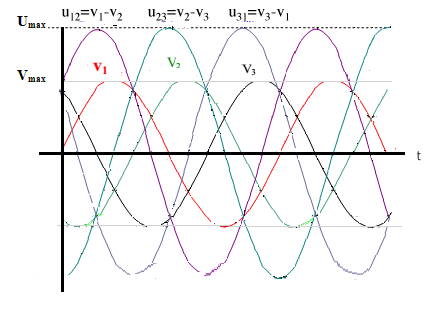
Représentation temporelle des tensions simples
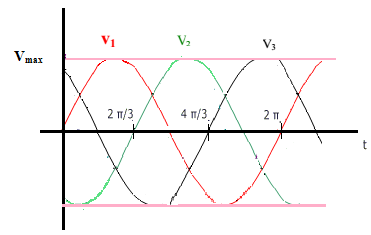
Écriture des tensions simples en complexe
V1 = [V, 0°] V2 = [V, -120°] V3 = [V, -240°]
Vecteurs de Fresnel associés
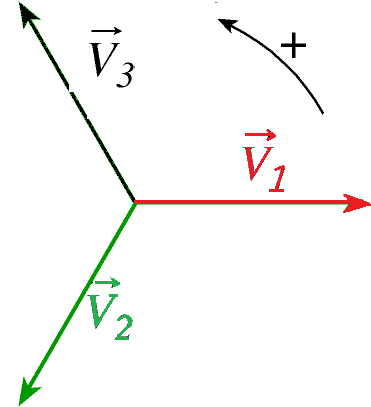
Tension Composée
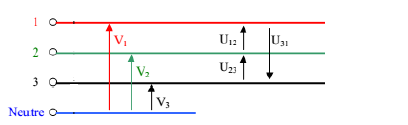
Tension composée : est la différence de potentiel entre 2 phases. Nous les noterons : u12(t),u23(t) et u31(t).
Avec u12(t) = v1(t) – v2(t) u23(t)= v2(t) – v3(t) u31(t)= v3(t) – v1(t)
Les trois tensions composées sont:
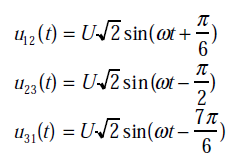
Représentation temporelle des tensions composées
Écriture des tensions composées en complexe
U12 =V1 – V2 = [V√3, + 30°]
U23 =V2 – V3 = [V√3, – 90°]
U31 =V3 – V1 = [V√3, + 150°]
Vecteurs de Fresnel associés
Représentation Vectorielle De FRESNEL Des Tensions :
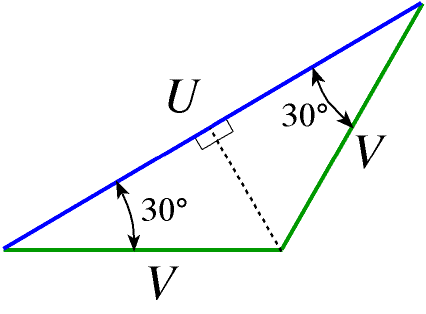
Relation entre U et V
U = 2V cos 30 soit U = 2V√3/2 Finalement : U = V√3
Propriétés importantes :
- La somme de trois grandeurs formant un système triphasé équilibré est nulle : V1+V2+V3=0
- La relation qui existe entre la valeur efficace V et U U= √3.V
RÉCEPTEURS TRIPHASÉS ÉQUILIBRÉS
Récepteurs triphasés : ce sont des récepteurs constitués de trois dipôles d’impédance Z.
Equilibré : si Z1 = Z2 = Z3 = Z .
Courant par phase : c’est le courant qui traverse les éléments Z du récepteur triphasé. Symbole : J
Courants en ligne : c’est le courant dans les fils du réseau triphasé. Symbole : I
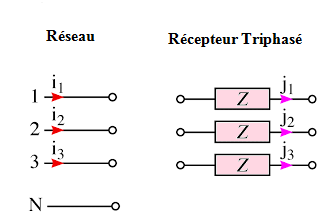
On peut relier le réseau et le récepteur de deux façons différentes : en étoile ou en triangle.
Couplage Étoile
Montage :
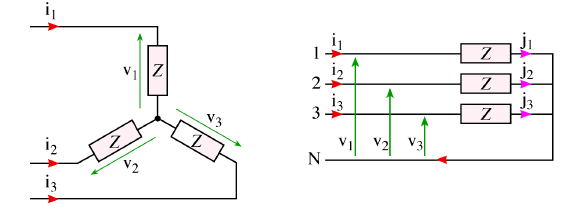
Les deux branchement sont les mêmes seulement représentés de deux façons différentes
Puisque les impédances sont identiques donc i1 + i2 + i3 = 0, alors iN = 0. le courant dans le fil neutre est nul. donc le fil neutre pas nécessaire.
le fil neutre ne sert à rien pour un système triphasé équilibré, .
Relations entre les courants :
On remarque que les courants en ligne sont égaux aux courants par phase.
i1 = j1 ; i2 = j2 ; i3 = j3
De plus puisque la charge et le réseau sont équilibrés, donc : I1 = I2 = I3 = I = J
A retenir le couplage étoile : I = J
Couplage Triangle
Montage

Les deux branchement sont identiques seulement représentés de deux façons différentes
Les courants qui circulent dans les impédances Z sont différents des courants de ligne
J12 est généré par La tension U12
J23 est généré par La tension U23
J31est généré par La tension U31
Puisque les impédances sont identiques donc i1 + i2 + i3 = 0 et j12 + j23 + j31 = 0
En couplage triangle le fil neutre n’est pas nécessaire.
Relations entre les courants :
- i2 = j23 – j12 => I2 = J23 – J12
- i1 = j12 – j31 => I1 = J12 – J31
- i3 = j31 – j23 => I3 = J31 – J23
Le système triphasé est équilibré donc : I1 = I2 = I3 = I et J1 = J2 = J3 = J.
la relation entre I et J est : I = √3 J
RÉCEPTEURS TRIPHASÉS DÉSÉQUILIBRÉS
Un récepteur est non équilibré si ses trois impédances Z1, Z2 et Z3 sont différentes, que ce soit couplé en étoile ou en triangle
Couplage Étoile Avec Neutre
La somme des trois courants en ligne n’est plus nécessairement nulle, donc on a un courant qui circule dans le conducteur de neutre
Couplage triangle
Puisque le système est déséquilibré alors la relation I =√3 J n’est plus valable car .
PUISSANCES EN TRIPHASÉ
Théorème De Boucherot
Les puissances active et réactive absorbées par un groupement de dipôles sont respectivement égales à la somme des puissances actives et réactives absorbées par chaque élément du groupement
On a donc P = P1+P2+P3 et Q = Q1+Q2+Q3
Charge Triphasée Déséquilibrée
En cas de charge déséquilibrée, tensions et courants sont déphasées de φ1, φ2 ou φ3 suivant les phases.
La puissance active est :P = V1.I1.cos φ1 + V2.I2.cos φ2 + V3.I3.cos φ3
Et la puissance réactive s’écrit alors : Q = V1.I1. sin φ1 + V2.I2. sin φ2 + V3.I3. sin φ3
Charge Triphasée Équilibrée
Si la charge est équilibrée, les trois impédances sont identiques, donc :
φ1 = φ2 = φ3 = φ ; V1 = V2 = V3 = V et I1 = I2 = I3 = I.
Pour un récepteur équilibré : P1=P2=P3 alors P = P1+P2+P3=3.P1
et Q1=Q2=Q3 donc Q=Q1+Q2+Q3=3.Q1
La puissance active a pour expression : P = 3.V.I.cos φ
La puissance réactive est : Q = 3.V.I.sin φ.
On peut exprimer la puissance active et la puissance réactive en fonction tension composée U
P = √3.U.I.cos φ Q = √3.U.I.sin φ S = √3.U.I
Mesure De Puissance En Triphasé
Mesure de la puissance active P
Ligne à 4 fils et circuit est équilibré
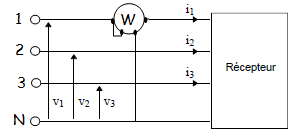
Lorsque le récepteur est équilibré, un seul wattmètre suffit pour mesurer la puissance active absorbée.
, c’est à dire on mesurer la puissance consommée par une phase et de multiplier par trois.
La puissance absorbée par le récepteur triphasé équilibré est P = 3P1
Ligne à 4 fils et circuit déséquilibré
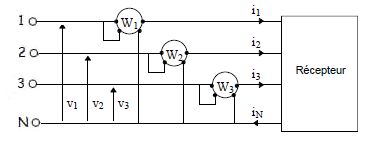
Il faut mesurer les puissances consommées par les trois phases et additionner.
Trois wattmètres sont nécessaires pour mesure la puissance active :
P = P1N + P2N + P3N
Ligne à 3 fils
Circuit équilibré ou déséquilibré
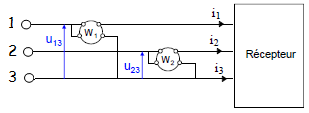
Pour un système déséquilibré ou un système équilibré dont le neutre n’est
pas accessible, on mesure la puissance active à l’aide de deux wattmètres.
On détermine la puissance active absorbée à l’aide de la relation : P = P1 + P2
AMÉLIORATION DU FACTEUR DE PUISSANCE « COS Φ «
Un facteur de puissance faible entraine :
- Une puissance apparente 𝑺 plus élevée
- Une consommation de l’énergie réactive 𝑸
- Une consommation d’énergie plus importante
Moyen utilisé pour relever le facteur de puissance : (Augmenter cos φ)
L’addition de condensateurs permet de réduire l’énergie réactive, on utilise une batterie de condensateurs que l’on raccorde aux bornes du récepteur ou de l’installation à compenser.
On utilise le montage triangle dans les réseaux BT (basse tension), et le montage étoile dans les réseaux HT (haute tension)
Relèvement Du Facteur De Puissance
Un bon facteur de puissance est que le cos φ proche de 1, minimum cos φ= 0,93
Couplage des condensateurs en triangle :
U:Tension aux bornes d’un condensateur
Puissance réactive absorbée par un condensateur : QC1 = – CωU2
Puissance réactive absorbée par les trois condensateurs : QC = 3QC1 = -3CωU2
Détermination de la capacité
On calcule la capacité du condensateur de la manière suivante:
QC = -3C.ω.U2 = Q’- Q
-3C.ω.U2 = P.tg φ’ – P.tg φ
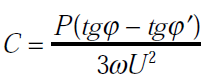
Couplage des condensateurs en étoile:
En utilisant le même raisonnement que précédemment, on montre que la capacité du condensateur est :
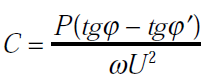
Commentaires
Enregistrer un commentaire