cours : les transformateurs monophasé

TRANSFORMATEURS MONOPHASÉS

 

Rôle

Un  transformateur permet  d’élever ou d‘abaisser une tension alternative selon le besoin de l’utilisation.

Symbole

Constitution  et Principe de Fonctionnement

Le transformateur est constitué essentiellement de :

• Un Circuit magnétique fermé  comportant deux noyaux (ou colonnes) et deux culasses  réunissant les noyaux. Il a pour rôle de canaliser le flux magnétique.

• Deux bobinages en cuivre sont placés sur les noyaux du circuit magnétique fermé: un enroulement primaire  de N1 spires , relié à la source alternative et un enroulement secondaire  de N2 spires

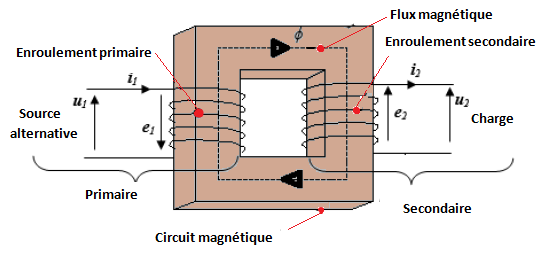
Le primaire est alimenté par une tension variable et donne naissance à un flux magnétique (Φ(t) alternatif)  variable dans le circuit magnétique feuilleté.

Le secondaire, soumis à la variation de ce flux, est le siège d’une force électromotrice (f.e.m) induite  due à la loi de Lenz (e = – N2 dΦ/dt).

Transformateur Parfait  

Un transformateur est parfait lorsqu’il ne provoque aucune perte d’énergie :

•  Les résistances des enroulements  primaire et secondaire  sont nulles , (pas de pertes par effet joule ).
• Le circuit magnétique fermé de perméabilité infinie donc pas de perte dans le circuit magnétique , pas de pertes de fer  ( ni hystérésis, ni courant de Foucault),  tout le flux du primaire se rend au secondaire

RELATIONS DU TRANSFORMATEUR PARFAIT.

Relations entre les tensions

A chaque instant, les deux enroulements primaire et secondaire sont traversées par le même flux magnétique.
( pas de fuites magnétiques)

Au primaire formé de N1 spires est le siège d’une f.e.m:

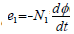
e1 = -u1 en complexe: U1 = j ω N1 Φ

Au secondaire formé de N2 spires est le siège d’une f.e.m:

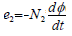
e2 =u2 en complexe: U2 = – j ω N2 Φ

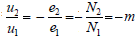
les tensions u1 et u2 sont en opposition de phase.

En valeur efficace :

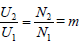
m: rapport de transformation du transformateur.

Relations entre les intensités .

Le transformateur est parfait donc son rendement est : η = P2/P1 = 1 alors P1 = P2

sachons que φ1 = φ2 donc on a : S1 = S2 = U1 I1 = U2 I2 ce qui implique :

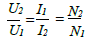
Diagramme de Fresnel

Les quatre grandeurs u1, i1, u2 et i2 sont toutes sinusoïdales : on peut introduire leurs vecteurs de Fresnel

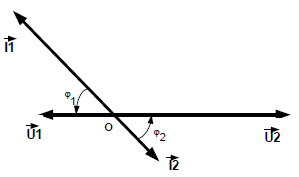
Les tensions u1 et u2 sont en opposition de phase avec u2 = – m.u1 en valeur efficace U2=mU1

Les courants i1 et i2 sont en opposition de phase avec i1 = – m.i2 en valeur efficace I1=mI2

Transformateur Réel

Pour le transformateur réel, on tient compte des grandeurs qui ont été négligées au cours d’étude d’un transformateur parfait

Le schéma équivalent du transformateur réel est :

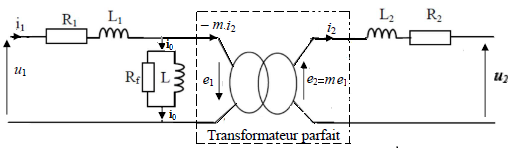
• R1 : résistance de l’enroulement primaire
• R2 : résistance de l’enroulement secondaire
• L1 : Inductance de l’enroulement primaire
• L2 : Inductance de l’enroulement secondaire
• Rf : résistance de circuit magnétique
• L : Inductance de circuit magnétique

On pose:

𝑋1 = L1 𝜔 : Réactance de fuites au primaire.
𝑋2 = L2 𝜔 : Réactance de fuites au secondaire

RELATIONS DU TRANSFORMATEUR RÉEL

Relations entre les tensions

L’ équation du circuit primaire s’écrit : U1 = – E1+R1 I1 + j𝑋1 I1
L’ équation du circuit secondaire s’écrit : U2 = E2– R2 I2 – j𝑋2 I2

Relations entre les intensités

Dans un transformateur réel pour le courant primaire on a l’expression:

i1 = i – m i2
i : courant absorbé par le primaire du transformateur à vide.

TRANSFORMATEUR RÉEL DANS L’APPROXIMATION DE KAPP

Hypothèse
L’hypothèse de Kapp permet de négliger le courant I devant le courant I1 ce qui revient à à débrancher l’impédance ( Rf // L ): le schéma équivalent devient :

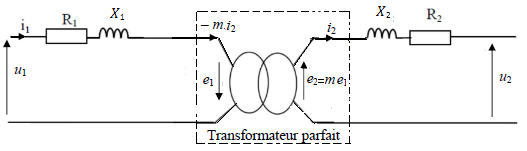
Schéma équivalent ramené au secondaire :

on peut ramener les éléments R1 et X1=L1.ω , situés initialement au primaire, vers le secondaire en les multipliant par m2. Le modèle équivalent obtenu, dit de Kapp qui est représenté sur le schéma suivant :

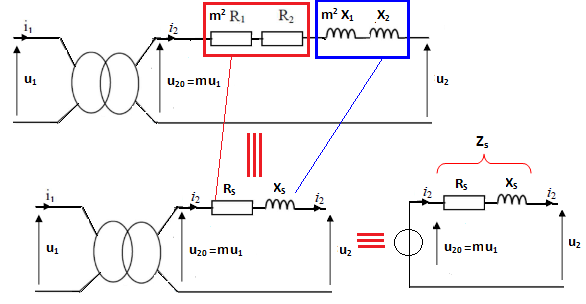
Avec RS = (R2+m2 R1) et XS = (X2 + m2 X1)

• RS : la résistance ramenée au secondaire
• XS : La réactance ramenée au secondaire

Voir aussi:  Cours Physique : Noyau, Masse et Energie

Le secondaire se comporte comme une source de:

• Tension. : U20=mU1
• Impédance : ZS = RS +j. XS ZS2 = RS2 +XS2 
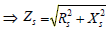
• U2 = U20 – ZS I2=U20 – ΔU2
  

ΔU2 = ZS I2 : valeur approché de la chute de tension au secondaire

Calcul approché de la chute de tension au secondaire :

On peut alors le réaliser à l’aide d’une formule approchée :
ΔU2 = RS.I2.cos φ2 + XS.I2.sin φ2

Détermination des paramètres et pertes du transformateur

On effectue deux essais :  essai à vide et essai en court-circuit  afin de déterminer:   

• m: rapport de transformation  
• RS : résistance de circuit magnétique
• XS : réactance magnétisante  
• Pfer : pertes fer
• Pj: pertes joules

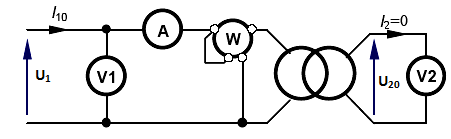
 Essai  à vide:

 sous tension nominale U1 = U1N on mesure U20 à l’aide de voltmètres

Par intermédiaire du wattmètre on mesure la puissance à vide  P  absorbées par le primaire:

cette puissance P représente les pertes à vide.

Calcul du rapport de transformation :

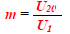
Détermination des pertes de fer

A vide la puissance consommée P est égale à la somme des pertes joules dans le
primaire et des pertes de fer

P = R1 I²+ Pfer

sachons que i1 = i – m i2

Puisque le courant secondaire est nul I2 = 0, donc I1 = I.

Comme I est très faible donc R1 I² est très faible devant Pfer alors on écrit P = Pfer

Les pertes joules est négligeable devant les pertes de fer

Essai en court-circuit

On amène le courant secondaire à une valeur nominale, tout en appliquant au primaire une tension réglable depuis 0 jusqu’à avoir une valeur nominale I2cc=I2n .

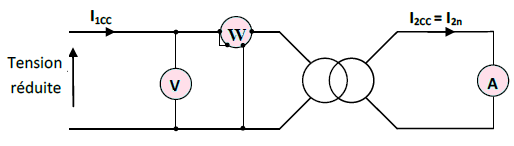
On relève les grandeurs suivantes :

• U1cc :Tension réduite primaire
• I2cc = I2n : Courant secondaire
• P1cc : Puissance primaire absorbée en court-circuit

Détermination de la résistance ramenée au secondaire Rs
Puisque l’on se place au régime nominal de courant, les pertes mesurées en court circuit sont nominales, appelées aussi pertes cuivre

comme U1cc << U1n les pertes fer sont négligeables devant les pertes Joule donc:

P1cc =RS I2cc2 d’où la résistance RS est donc:

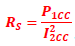
Calcul de réactance XS

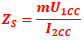
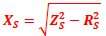
Rendement du transformateur

Le rendement est le rapport :

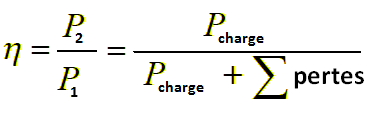
On peut le déterminer à l’aide des deux wattmètres pour les faibles puissances, pour les grandes puissances on utilise la méthode des pertes séparées . La relation utilisée est la suivante :

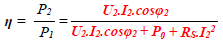
P1:Puissance à l’entrée

P2: Puissance de charge

P : perte de fer

Pj: perte de joule =RS I22